Geometry: The ancient Egyptians and Mesopotamians developed methods of measuring objects and calculating relations that they used to build monuments like the pyramids. The Greeks called this geometry, which means earth- measurement. About 300BC, a Greek called Euclid, who lived in Egypt, developed proofs of the geometric rules that the Egyptians had devised. Euclid's proofs started from axioms and reasoned logically from them to conclusions. This has been seen by some philosophers as a model for what science (or part of Science) should be. Hobbes argued for a Social Science based on Euclidian methods. Poincare used Euclidian and other geometries to argue that science is based on imagination.
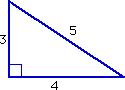
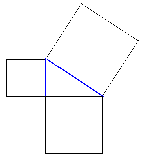
The Egyptians, who discovered the 3,4,5 rule, used it to build pyramids. The 3,4,5 rule is connected to these numbers: 5 x 5 = 25 (the square of 5)
4 x 4 = 16 (the square of 4)
16 + 9 = 25 (4 squared, plus 3 squared, equals 5 squared)
|
Maths index ***************** Geometry 
|
|||||||||||
Euclid's Axioms
Euclid's axiomatic foundations for geometry contained:several definitions,
some postulates and
a few common notions.
3. The extremities of a line are
points
4. A straight line is a line which lies evenly with the
points
on itself
6. The extremities of a surface are lines
7. A plane surface is a surface which lies evenly with the
straight lines on itself.
9. And when the lines containing the angle are straight, the angle is
called rectilinear.
Euclid's definitions
1. A point is that which has no part
2. A line is breadthless length
5. A surface is that which has length and breadth only
8. A plane angle is the inclination to one another of two lines
in a plane which meet one another and do not lie in a straight line.
11. An obtuse angle is an angle greater than a right angle.
12. An acute angle is an angle less than a right angle.
13. A boundary is that which is an extremity of anything.
14. A figure is that which is contained by any boundary or
boundaries.
|
See circle formula math2.org |
16. And the point is called the centre of the circle.
17. A diameter of the circle is any straight line drawn through
the centre and terminated in both directions by the circumference
[boundary]
of the
circle, and such a straight line also bisects the circle.
18. A semicircle is the figure contained by the diameter and the
circumference cut of by it.
19. Rectilineal figures are those which are contained by
straight lines, trilateral figures being those contained by three,
quadrilateral those contained by four, and multilateral those
contained by more than four straight lines.
20. Of trilateral figures, an equilateral triangle is that which
has its three sides equal, an isosceles triangle that which has two
of its sides alone equal, and a scalene triangle that which has its
three sides unequal.
21. Further, of trilateral figures, a right-angled triangle is
that which has a right angle, an obtuse-angled triangle that which
has an obtuse angle, and an acute-angled triangle that which has its
three angles acute.
22. Of quadrilateral figures, a square is that which is both
equilateral and right-angled: an oblong that which is right angled
but not equilateral; a rhombus that which is equilateral but not
right angled; and a rhomboid that which has its opposite sides and
angles equal to one another but is neither equilateral nor right-angled.
And let quadrilaterals other than these be called trapezia.
23.
Parallel straight lines are straight lines which, being in the
same
plane and being produced indefinitely in both directions, do not meet one
another in either direction.
Study
links outside this site
Andrew Roberts' web Study Guide
Picture introduction to this site
Top of
Page
Take a Break - Read a Poem
Click coloured words to go where you want
Andrew Roberts likes to hear from users:
To contact him, please
use the Communication
Form